A osmose é a passagem de solvente (geralmente a água) por uma membrana semipermeável para um meio mais concentrado. Já a pressão osmótica é a pressão que deve ser exercida sobre um sistema para evitar que a osmose ocorra.
Por exemplo, observe o tubo em U apresentado a seguir. Do lado esquerdo, há somente água pura, e, do lado direito, há uma solução. Elas estão separadas por uma membrana semipermeável. Com o tempo, a osmose começa a ocorrer e o solvente do lado esquerdo começa a passar para a solução do lado direito até que a altura da solução exerce uma pressão sobre a membrana que impede que o solvente continue passando por ela, por essa razão, a osmose para. Essa pressão é a pressão osmótica.
.jpg)
Osmose ocorrendo em tubo em U
Se quiséssemos que essa osmose não tivesse nem ao menos começado, era só ter exercido, no início, uma pressão sobre o lado direito do tubo (sobre a solução) com intensidade igual à pressão osmótica para a solução em questão. Desse modo, o fluxo de solvente ficaria impedido e a osmose não ocorreria, como está sendo feito na imagem a seguir:
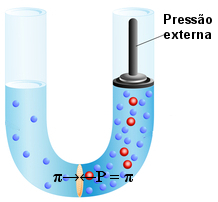
Pressão osmótica aplicada para impedir osmose
Quanto mais concentrada for a solução ou quanto maior for a diferença de concentração entre as duas soluções que estão separadas por uma membrana semipermeável, maior será a pressão osmótica que deverá ser exercida para que a osmose não ocorra.
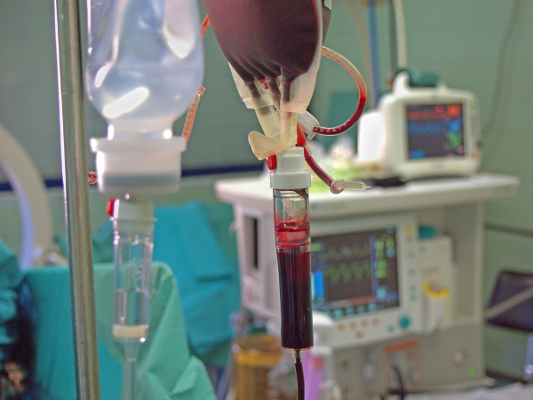
Essas informações são muito importantes em nosso cotidiano. Por exemplo, o soro fisiológico deve ter a mesma pressão osmótica que o sangue (aproximadamente 7,7 atm), ou seja, deve ser isotônico em relação ao sangue. Caso contrário, sérios danos poderiam ser causados ao organismo.
Se o soro fosse hipertônico em relação ao sangue, isto é, se sua concentração e pressão osmótica fossem maiores que as do sangue, os glóbulos vermelhos murchariam, pois perderiam água, que seria “sugada” para o lado de fora. Por outro lado, se o soro fosse hipotônico em relação ao sangue (se sua concentração e pressão osmótica fossem menores que as do sangue), a água passaria a entrar dentro dos glóbulos vermelhos e elas inchariam, podendo até estourar, o que é conhecido como hemólise.
Na natureza, esses conceitos também são vistos. Por exemplo, você já se perguntou como a água consegue vencer a barreira da gravidade e chegar até o topo de árvores muito altas? Isso é possível porque a pressão osmótica nas raízes das plantas pode atingir valores bem altos, o que permite que a água movimente-se através de todas as regiões da planta.

A pressão osmótica das raízes das árvores permite que a água chegue até as suas partes mais elevadas
Visto que a pressão osmótica muda de acordo com a concentração da solução, como podemos calcular qual é o seu valor?
Bem, isso foi determinado pelo físico e químico holandês Jacobus Henricus Van’t Hoff (1852-1911). Ele observou que a pressão osmótica dependia das mesmas variáveis que participam da Equação de Estado dos Gases (Equação de Clapeyron). Veja como isso é verdade: sabemos que a pressão osmótica depende da concentração em quantidade de matéria (em mol/L), que é dada por:
Concentração em quantidade de matéria (mol/L) = quantidade de matéria do soluto (mol)
volume da solução (L)
ou
M = n1
V
Além disso, a temperatura (T) também influencia na pressão osmótica. Observe que aparecem as seguintes grandezas: pressão (P), volume (V), quantidade de matéria (n) e temperatura (T), ou seja, as mesmas variáveis da equação de Clapeyron mostrada a seguir:
P . V = n . R . T
A pressão osmótica é simbolizada por π, assim, substituindo a pressão na equação acima, temos:
π . V = n . R . T
π = n . R . T
V
Visto que M = n , podemos escrever essa equação da seguinte forma:
V
π = M . R . T
Lembrando que R é a constante universal dos gases perfeitos, cujo valor é 0,082 atm . L . K-1 . mol-1 ou 62,3 mmHg . L . K-1 . Mol-1. Essa é, então, a fórmula que pode ser usada para calcular a pressão osmótica (π) para soluções moleculares.
No caso de soluções iônicas, deve-se acrescentar o fator de Van't Hoff (i), que é a relação feita entre o número total de partículas finais em relação às iniciais nas soluções iônicas.
Por exemplo, se adicionarmos 1 mol de NaCl na água, teremos no final 1 mol de partículas de Na+ e 1 mol de partículas de Cl-, conforme mostra a equação de ionização do sal a seguir:
NaCl → Na+(aq)+ Cl-(aq)
1 mol → 1 mol + 1 mol } 2 mols
Se o grau de ionização é de 100%, então o fator de Van't Hoff é igual a 2 nesse caso.
Assim, a equação fica do seguinte modo:
π = M . R . T . i
Veja um exemplo de como calcular a pressão osmótica:
Exemplo: Eventualmente, a solução de glicose 0,3 mol/L é utilizada em injeção intravenosa, pois tem pressão osmótica próxima à do sangue. Qual é a pressão osmótica, em atmosferas, dessa solução a 37ºC? Dado: R = 0,082 atm . L . K-1 . mol-1.
Resolução:
Dados:
M = 0,3 mol/L
R = 0,082 atm . L . K-1 . mol-1
T = 37ºC (temos que passar para graus kelvin, pois a constante universal dos gases perfeitos, R, está nessa unidade. Para tal, basta somar a temperatura em graus Celsius com 273) = 310 K.
Π = ?
Como é uma solução de glicose, ou seja, é uma solução molecular, não precisamos usar o fator de Van't Hoff. Assim, basta aplicar os valores dados na fórmula:
π = M . R . T
π = (0,3 mol/L). (0,082 atm . L . K-1 . mol-1) . (310 K)
π =7,63 atm
Aproveite para conferir a nossa videoaula sobre o assunto: