O texto Transformações gasosas mostrou as três possíveis transformações que podem ocorrer com uma massa fixa de determinado gás em condições ideais. Resumidamente, temos:

Resumo das três transformações gasosas
Podemos, então, unir todas essas leis em uma mesma equação que relacione as três grandezas físicas dos gases (pressão, temperatura e volume):
P . V = k
T
ou
P1 . V1 =P2 . V2
T1 T2
Essa é a equação geral dos gases. Veja como ela relaciona a proporcionalidade entre essas três grandezas:
-
A pressão e o volume são inversamente proporcionais, se um aumenta, o outro diminui e vice-versa;
-
A pressão e a temperatura são diretamente proporcionais, se uma aumenta, a outra também aumenta e vice-versa;
-
A temperatura e o volume são diretamente proporcionais, se um aumenta, o outro também aumenta e vice-versa.
Assim, quando ocorre alguma transformação gasosa, podemos usar essa equação geral dos gases para descobrir qual é a variação que houve nas grandezas. Lembrando que a massa do gás deve ser fixa e estar nas Condições Normais de Temperatura e Pressão (CNTP), em que:
Pressão = 1 atm ou 760 mmHg
Temperatura = 0 ºC = 273 K
Além disso, as relações estabelecidas nessa equação geral de transformação dos gases somente serão verdadeiras se a temperatura estiver na escala kelvin (K).
Veja um exemplo:
(FMIt-MG) Considere o diagrama:
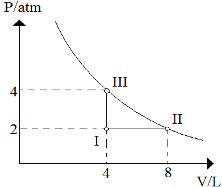
Diagrama de transformação gasosa
Responda:
a) Qual é o nome das transformações gasosas verificadas quando passamos de I para II, de II para III e de III para I?
b) Se a temperatura em II é igual a 227 ºC, qual é a temperatura em III e em I?
Resolução:
a) De I para II: Visto que a pressão permaneceu constante em 2 atm, temos uma transformação isobárica;
De II para III:Visto que a temperatura permaneceu constante, o volume variou de 8 L para 4 L e a pressão variou de 2 atm para 4 atm, temos uma transformação isotérmica;
De III para I:Visto que o volume permaneceu constante em 4 L, temos uma transformação isocórica ou isovolumétrica.
b) Lembre-se de que a temperatura deve estar na escala kelvin. Assim, temos:
TK = TºC + 273
TK = 227 + 273
TK = 500 K
Agora vamos usar a equação geral dos gases para descobrir a temperatura em III e em I:
|
PII . VII = PIII . VIII 2 . 8 = 4 . 4 2 . 8 . TIII = 500 . 4 . 4 16 TIII = 8000 TIII = 8000 TIII = 500 K = 227ºC |
PII . VII = PI . VI 2 . 8 = 2 . 4 2 . 8 . TI = 500 . 2 . 4 16 TI = 4000 TI =4000 T1 = 250 K = -23 ºC |
Observe que as temperaturas em II e em III eram iguais, confirmando que de II para III ocorreu uma transformação isotérmica.
Por Jennifer Fogaça
Graduada em Química